Full-linear vehicle modelling
> restart: libname := libname, "C:/MBSymba": with(MBSymba_r6):
LA:=LinearAlgebra:

> PDEtools[declare]({x(t),y(t),u(t),v(t),psi(t),omega(t),delta(t),Ff(t), Fr(t)},prime=t,quiet);
Definition of small variables
> linear_modeling({v(t),y(t),psi(t),omega(t),delta(t)},{},{Fr(t),Ff(t)});
Warning, Linear Modeling option has been choosen for the following variables:
![]()
Definition of the Moving Frame
The forward speed U is assumed constant
> use_moving_frame(U,v(t),0,0,0,omega(t)):
Warning, The base frame <moving_frame> has been selected.
vehicle chassis
define main frame
> TV := moving_frame:
define vehicle body
> vehicle := make_BODY(TV,M,IX,IY,IZ): show(vehicle,'synthetic');


rear tire
> R := make_POINT(TV,-b,0,0): show(R);

rear tire kinematics
> VR:=velocity(R):show(VR);

> lambda[R] := linearize( -arctan( comp_Y(VR,TV)/comp_X(VR,TV) )):
force
> Fr := KLr * lambda[R];
make_VECTOR(TV, 0, Fr ,0):
rear_tire := make_FORCE(%, R, vehicle): show(rear_tire);
![]()

front tire
> TF := TV * Translate(a,0,0) * Rotate('Z',delta(t));

contact point
> F := origin(TF): show(F,'synthetic');

front tire kinematics
> VF := project(velocity(F),TF): show(VF);
> lambda[F] := linearize ( -arctan( comp_Y(VF,TF)/comp_X(VF,TF) ) );

![]()
force
> Ff := KLf * lambda[F];
make_VECTOR(TF, 0, Ff ,0):
front_tire := make_FORCE(%, F, vehicle): show(front_tire);
![]()

Newton-Euler equations
Newton
> eqnsN := newton_equations({vehicle,rear_tire,front_tire}): show(eqnsN);

Euler
> eqnsE := euler_equations({vehicle,rear_tire,front_tire},CoM(vehicle)):
show(eqnsE);
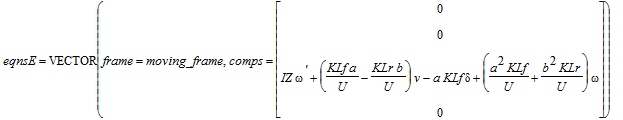
State space formulation
implicit state equations
> lin_eqns := [comp_Y(eqnsN), comp_Z(eqnsE)]: Vector(lin_eqns);
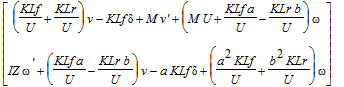
state variables
> xx := [v(t),omega(t)];
system inputs
> uu := [delta(t)];
state space formulation
> AA,BB := state_space(lin_eqns,t,xx,uu);
AA,BB := map(simplify,AA),BB;
![]()
![]()
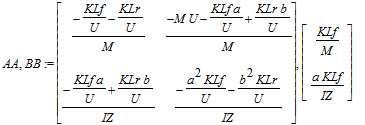
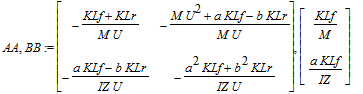
> Vector(diff(xx,t)) = AA,Vector(xx) ; BB,Vector(uu);


UnderSteering Vehicle
> interface(displayprecision=2):
define vehicle characteristics
> understeer_vehicle :=[
a=1.3, from Cr to G
b=1.3, from G to Cf
M=1000.,mass
IZ=600,yaw inertia
KLr=24.*5000,rear tire cornering stiffness
KLf=20.*5000 front tire cornering stiffness
];
AN := map(expand,subs(understeer_vehicle,AA));
BN := subs(understeer_vehicle,BB);
![]()

![]()
Free Stability
> free_stability := speed -> LA[Eigenvalues](subs(U=speed,AN));
![]()
> free_stability (10);
![]()
> free_stability (30);
![]()
> free_stability (50);
![]()
Eigenvalues from 1 to 50 m/s
> max_speed := 60; maximum speed
> for i from 1 to max_speed do
ev := free_stability(i):
ev1[i]:=ev[1]: ev2[i]:=ev[2]:
end do:
ev1 := convert(ev1,list):
ev2 := convert(ev2,list):
![]()
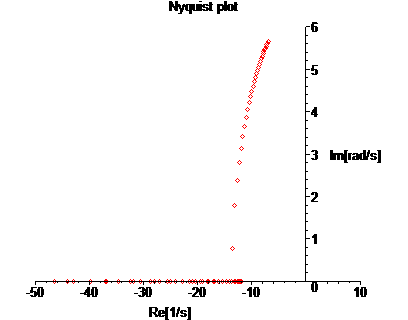
Nyquist
> plots[complexplot]([op(ev1),op(ev2)],style=point,view=[-50..10,0..6],labels=["Re[1/s]","Im[rad/s]"],title="Nyquist plot");
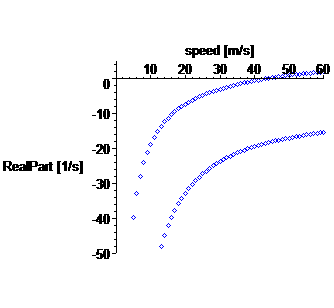
> plot([seq([i,Re(ev1[i])],i=1..max_speed), seq([i,Re(ev2[i])],i=1..max_speed)],
style=point,view=[0..max_speed,-50..5],color=[blue,red],labels=["speed [m/s]","RealPart [1/s]"]);

OverSteering Vehicle
define vehicle characteristics
> oversteer_vehicle :=[
a=1.3, from Cr to G
b=1.3, from G to Cf
M=1000.,mass
IZ=600.,yaw inertia
KLr=18.*5000,rear tire cornering stiffness
KLf=24.*5000 front tire cornering stiffness
];
> AN := map(expand,subs(oversteer_vehicle,AA));
BN := subs(oversteer_vehicle,BB);
![]()
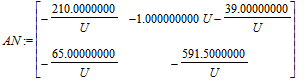
![]()
Free Anaylsis
> free_stability (10);
![]()
> free_stability (30);
![]()
> free_stability (50);
![]()
Eigenvalues from 1 to 50 m/s
> max_speed := 60; maximum speed
> for i from 1 to max_speed do
ev := free_stability(i):
ev1[i]:=ev[1]: ev2[i]:=ev[2]:
end do:
ev1 := convert(ev1,list):
ev2 := convert(ev2,list):
![]()
Nyquist
> #plots[complexplot]([op(ev2),op(ev2)],style=point,view=[-60..10,0..6],labels=["Re[1/s]","Im[rad/s]"],title="Nyquist plot");
> plot([seq([i,Re(ev1[i])],i=1..max_speed), seq([i,Re(ev2[i])],i=1..max_speed)],
style=point,view=[0..max_speed,-50..5],color=[blue,red],labels=["speed [m/s]","RealPart [1/s]"]);