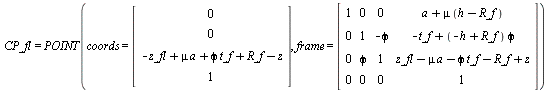by Roberto Lot and Nicola Dal Bianco.
In this page a car multibody model with 14 mechanical degrees of freedom (dof) is presented. This model includes: chassis motion (6 dof), suspensions (4 dof) and wheels spin (4 dof).
This model is the one used in the 2015 IAVSD conference paper “The significance of high-order dynamics in lap time simulations“, whose abstract is the following:
“This work aims to study which level of detail should be preserved in the multibody modelling of a racing car in order to obtain reliable results without excessive model complexity. Three multibody models have been developed and compared through optimal control simulations. The models differ from each other for the order of dynamics comprised: starting from a 14 degrees of freedom (dof) car which includes chassis and wheels motion, a 10 dof model model is obtained by neglecting the wheels hop dynamics, finally a 7 dof model is derived by completely eliminating the suspension motion. Optimal control problem simulations, including parametric analyses varying the center of mass position and suspensions stiffness, have been executed on a full lap on the International circuit of Adria. Simulations results show that the 10 dof model gives almost the same results of the 14 dof one, while significantly reducing the computing time. On the contrary, the basic 7 dof model highlights remarkable differences in both the parametric analysis, suggesting the dynamics has been over-simplified.”
The description of the car multibody model now follows.
Model definition
> restart: printlevel:=3: interface(rtablesize):=30:
> with(MBSymba_r6):
PDEtools[declare]( prime=t,quiet):
> shortname := proc() PDEtools[declare](seq(args[i],i=1..nargs), seq(make_dot(args[i]),i=1..nargs), prime=t,quiet) end:
variable list
> grossmotion_vars := [V(t),lambda(t),Omega(t)]: in-plane dof
chassis_vars := [z(t),phi(t),mu(t)]: chassis degrees of freedom
1st index: f(ront) or r(erar); 2nd index: l(eft) or r(igth);
> wheels_spin := [theta_rr(t), theta_rl(t),theta_fr(t),theta_fl(t)]: wheels spin
> theta_rr_dot := omega_rr: theta_rl_dot := omega_rl: theta_fr_dot := omega_fr: theta_fl_dot := omega_fl: rename angular speed for convenience
> suspensions_vars := [z_rr(t),z_rl(t),z_fr(t),z_fl(t)]: suspensions dof (vertical travel)
> slip_vars := [ Lambda_rr(t), Lambda_rl(t), Lambda_fr(t), Lambda_fl(t), sideslip angles
Kappa_rr(t), Kappa_rl(t), Kappa_fr(t), Kappa_fl(t)]: longitudinal slip
> modelvars := [op(grossmotion_vars),op(chassis_vars),op(wheels_spin),op(suspensions_vars)]; all model mechanical vars
> shortname(modelvars);
(1.1.1)
> Freeze:= x -> simplify(eval(subs(seq(modelvars[i]=0,i=1..nops(modelvars)),x))):
Definition of the moving frame, located below the chassis center of
mass
> u(t) := V(t)*cos(lambda(t)): v(t) := -V(t)*sin(lambda(t)): NB: using 
explicitely makes it easy to assume it to be infinitesimal
> use_moving_frame(u(t),v(t),0,0,0,Omega(t)):
> T0 := moving_frame:
Warning, The base frame <moving_frame> has been selected.
Simplificative assumptions
The following variables and their derivative are assumed to be small
> linear_modeling({phi(t),mu(t),z(t),op(suspensions_vars)},{lambda(t),delta(t)}, {}):
Warning, Linear Modeling option has been choosen for the following variables:
Warning, Please be aware that when small and large variables are mixed, expressions of kinetic energy, Lagrange's equations, etc. may loose some terms.
Chassis
> TV := T0 * Translate(0,0,z(t)-h) * Rotate('X',phi(t)) * Rotate('Y',mu(t)); set_frame_name(TV,'TV'):
(1.1.1.1)
Center of mass
> G := origin(TV):
Chassis
> chassis := make_BODY(G, M, Ixx, Iyy, Izz, 0, Ixz, 0): show(chassis);
> show(acceleration(CoM(chassis)));
> CoM_acc := comp_XYZ(acceleration(CoM(chassis)),moving_frame ):
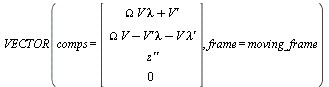(1.1.1.2)
Suspensions and Wheels
Procedura per compensare le inerzie che verrebbero aggiunte due volte
> anti_body := proc(BB::BODY)
local anti_BB:
anti_BB := copy(BB):
anti_BB[frame] := map(evalm,subs( seq(args[i],i=2..nargs), BB[frame])):
anti_BB[mass] := -BB[mass]:
anti_BB[inertia] := evalm(-BB[inertia]):
copy(anti_BB):
end:
Procedure to create the wheel body
> make_WHEEL := proc(sx::symbol,WCx,WCy,WCz, TM::frame)
#sx wheel suffix (i.e rr,rl,fr,fl)
#WCx,WCy,WCz wheel center coordinates (WCz wrt TV)
#TM, suspension roto-translation frame
#lock_vars vars to be zeronized in order to lock the suspension dofs
local TW, anti_w, wheel_torque, suspension_force;
> wheel frame
TW := TV * translate(WCx,WCy,WCz) * TM * rotate('Y',-mu(t) - cat(theta_,sx)(t)):
> wheel body
wheel_||sx := make_BODY(TW,m_w||sx,0,Iw_||sx,0);
> anti wheel body
anti_w := anti_body(wheel_||sx, seq(susp_sec_vars[i]=0,i=1..nops(susp_sec_vars)), z_||sx (t)=0, cat(theta_,sx)(t)=0):
> wheel torque
wheel_torque := make_TORQUE(subs(cat(theta_,sx)(t)=0, TW), cat(WT_,sx,_x), cat(WT_,sx,_y)(t), cat(WT_,sx,_z), chassis, wheel_||sx):
> suspension force
#RSx,RSy #constraint force
#FSa #elastic-damping suspension force
make_VECTOR(TV, 0, 0, cat(FSa_,sx)):
suspension_force := make_FORCE(%, CoM(wheel_||sx), chassis, wheel_||sx):
> output
copy(wheel_||sx), copy(anti_w), copy(wheel_torque), copy(suspension_force):
end:
Rear right wheel
Wheel frames
> TR_rr := Translate(0, 0,z_rr(t));
(1.1.2.1.1)
> m_wrr := mw_r: Iw_rr:=Iw_r:
(wheel_rr, anti_wheel_rr,wheel_torque_rr, suspension_force_rr) := make_WHEEL(rr,-b,t_r,h-R_r, TR_rr): show(wheel_rr);
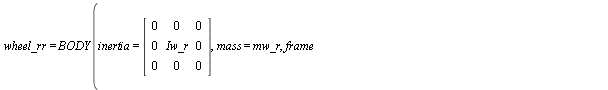
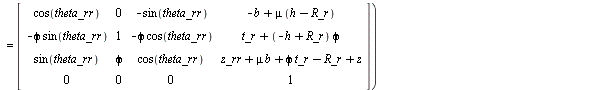(1.1.2.1.2)
wheel center
> WC_rr := project(CoM(wheel_rr),moving_frame): show(%),show(Freeze(WC_rr));
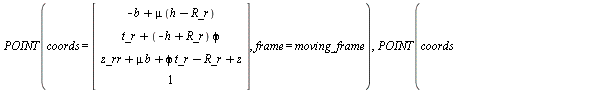
(1.1.2.1.3)
suspension force
> show(suspension_force_rr);
(1.1.2.1.4)
Rear Left wheel
Wheel frames
> TR_rl := Translate(0, 0,z_rl(t));
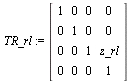(1.1.2.2.1)
> m_wrl := mw_r: Iw_rl:=Iw_r:
> (wheel_rl, anti_wheel_rl,wheel_torque_rl,suspension_force_rl):= make_WHEEL(rl,-b,-t_r,h-R_r, TR_rl):
> show(wheel_rl);
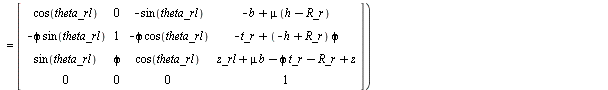(1.1.2.2.2)
Wheel center
> WC_rl := project(CoM(wheel_rl),moving_frame): show(%), show(Freeze(%));
(1.1.2.2.3)
suspension force
> show(suspension_force_rl);
(1.1.2.2.4)
Front right wheel
Wheel frames
> TR_fr := Translate(0, 0,z_fr(t));
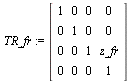(1.1.2.3.1)
> m_wfr := mw_f: Iw_fr:=Iw_f:
> (wheel_fr, anti_wheel_fr, wheel_torque_fr, suspension_force_fr) := make_WHEEL(fr,a,t_f,h-R_f, TR_fr): show(wheel_fr);
(1.1.2.3.2)
> WC_fr := project(CoM(wheel_fr),moving_frame): show(%), show(Freeze(%));
(1.1.2.3.3)
suspension force
> show(suspension_force_fr);
(1.1.2.3.4)
Front Left wheel
Wheel frames
> TR_fl := Translate(0, 0,z_fl(t));
(1.1.2.4.1)
> m_wfl := mw_f: Iw_fl:=Iw_f:
(wheel_fl, anti_wheel_fl, wheel_torque_fl,suspension_force_fl) := make_WHEEL(fl,a,-t_f,h-R_f, TR_fl): show(wheel_fl);
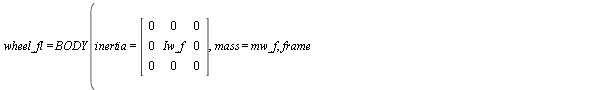
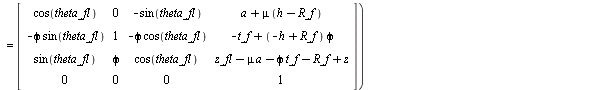(1.1.2.4.2)
> WC_fl := project(CoM(wheel_fl),moving_frame): show(%), show(Freeze(%));
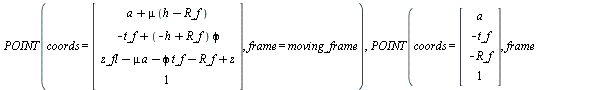
(1.1.2.4.3)
suspension force
> show(suspension_force_fl);
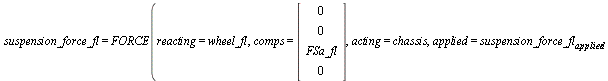
(1.1.2.4.4)
Tires forces and kinematics
build tire procedure
> with(MBSymba_r6_tire):
> build_TIRE := proc(_wheel::BODY, sx::symbol)
local tire,CP,TF,TT, VS,VN,VR, xi,tire_def, _lambda,kappa;
> tire := make_TIRE(_wheel, 0, R_||sx, 0,0, -xi(t), S_||sx,F_||sx,-N_||sx): #show(tire); tire used to calculate forces
> (CP,VS,VN,VR) := tire_kinematics(tire):
find the tire radial deformation
> tire_def := solve({comp_Z(CP, moving_frame)}, xi(t));
CP[coords] := linearize(subs(tire_def, CP[coords])); update Z component
slips
> VS := linearize(subs(tire_def,VS));
> VN := linearize(subs(tire_def,VN));
> VR := linearize(subs(tire_def,VR));
> _lambda := -VN/VS; _lambda := simplify(linearize(_lambda)):
> kappa := -VR/VS-1; kappa := simplify(linearize(kappa)):
> (TF,TT) := tire_forces(tire): show(TF); show(TT);
TF[comps] := collect( linearize(subs(tire_def, TF[comps])) , [S_||sx,F_||sx,N_||sx] ):
TT[comps] := collect( linearize(subs(tire_def, TT[comps])) , [S_||sx,F_||sx,N_||sx] ):
output
copy(CP), contact point
copy(TF), copy(TT), tire force and torque
rhs(op(tire_def)), tire radial deformation
_lambda, tire[roll], kappa, sideslpi, roll and longitudinal slip
VS:
> end:
Rear right tire
> R_rr:=R_r: wheel nominal radius
(CP_rr, tire_force_rr, tire_torque_rr, xi_rr, lambda_rr, camber_rr, kappa_rr, VS_rr) := build_TIRE(wheel_rr, rr):
> show(CP_rr);
(1.1.3.1.1)
> show(tire_force_rr); show(tire_torque_rr);
(1.1.3.1.2)
> show(Freeze(CP_rr)), show(Freeze(tire_force_rr));
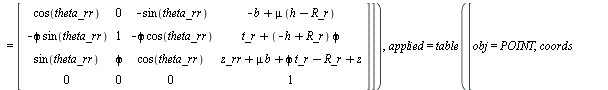
(1.1.3.1.3)
tire deformation
> xi_rr;
(1.1.3.1.4)
slip
> <'lambda_rr'=lambda_rr, 'camber_rr'=camber_rr, 'kappa_rr'=kappa_rr>;
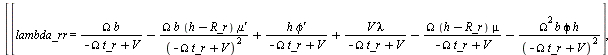
(1.1.3.1.5)
Rear left tire
> R_rl:=R_r: wheel nominal radius
(CP_rl, tire_force_rl, tire_torque_rl, xi_rl, lambda_rl, camber_rl, kappa_rl, VS_rl) := build_TIRE(wheel_rl, rl):
> show(CP_rl); #contact point
> xi_rl;#tire deformation
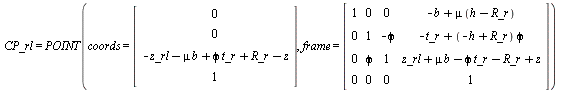
(1.1.3.2.1)
Front right tire
> R_fr:=R_f: wheel nominal radius
(CP_fr, tire_force_fr, tire_torque_fr, xi_fr, lambda_fr, camber_fr, kappa_fr, VS_fr) := build_TIRE(wheel_fr, fr):
> show(CP_fr); #contact point
> xi_fr; tire deformation
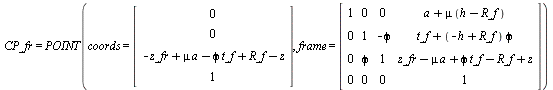
(1.1.3.3.1)
slip
> <'lambda_fr'=lambda_fr, 'camber_fr'=camber_fr, 'kappa_fr'=kappa_fr>;
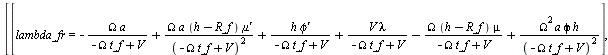
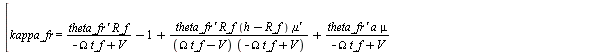
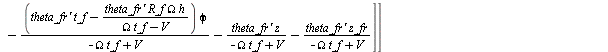(1.1.3.3.2)
(1.1.3.4.1)Aerodynamic Forces
Drag:
> ADp := copy(G): Point of the center of the body drag force (car CoM)
> make_VECTOR(T0, -Drag, 0, 0):
> ADf := make_FORCE(%,ADp,chassis): #show(%);
Lift:
> ALFp := copy(G): Point of the center of the front lift force (car CoM)
> make_VECTOR(T0, 0, 0, Lift):
> ALFf := make_FORCE(%,ALFp,chassis): #show(%);
Equations of motion
Chassis equations
Assembly multibody system
> bodies := {chassis, wheel_rr, wheel_rl, wheel_fr, wheel_fl,
anti_wheel_rr, anti_wheel_rl, anti_wheel_fr, anti_wheel_fl};
forces := {tire_force_rr,tire_torque_rr, tire_force_rl,tire_torque_rl,
tire_force_fr,tire_torque_fr, tire_force_fl,tire_torque_fl,
ADf, ALFf,
suspension_force_rr, suspension_force_rl, suspension_force_fr, suspension_force_fl };
(1.2.1.1)
Acceleration due to the gravity
> _gravity := make_VECTOR(master_frame,gx,0,g): show(_gravity);
(1.2.1.2)
Newton'e Equations
> eqnsN := newton_equations(bodies union forces):
> eqnsN[comps] := collect(eqnsN[comps],[M,m_wf,m_wr,N_]):
#<simplify([comp_XYZ(eqnsN,T0)])>; Removing secondary suspension motions
> <comp_XYZ(eqnsN,T0)>;
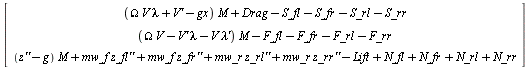(1.2.1.3)
Euler's Equations
> A := origin(moving_frame):
> eqnsEA := simplify(euler_equations(bodies union forces,A),size):
> <comp_XYZ(eqnsEA,moving_frame)>;
(1.2.1.4)
Wheels - Suspensions equation
> suspensions_vars;
(1.2.2.1)
> gen_susp_lag_eq := proc(sx::symbol)
lagrange_equations({wheel_||sx},z_||sx(t),t) - subs(z_||sx(t)=0, generalized_force({tire_force_||sx,tire_torque_||sx,suspension_force_||sx},z_||sx(t),t));
simplify(expand(%));
collect(%,{N_||sx,S_||sx,F_||sx,FSa_||sx, m_||sx});
end:
> susp_eqns := [ gen_susp_lag_eq(rr),
gen_susp_lag_eq(rl),
gen_susp_lag_eq(fr),
gen_susp_lag_eq(fl)
]:<%>;
(1.2.2.2)
Wheel spin equations
Euler equations
> eqnsEA_wrr := euler_equations({wheel_rr, tire_torque_rr, wheel_torque_rr}, CoM(wheel_rr)): #show(eqnsE_wrr);
> eqnsEA_wrl := euler_equations({wheel_rl, tire_torque_rl, wheel_torque_rl}, CoM(wheel_rl)):
> eqnsEA_wfr := euler_equations({wheel_fr, tire_torque_fr, wheel_torque_fr}, CoM(wheel_fr)):
> eqnsEA_wfl := euler_equations({wheel_fl, tire_torque_fl, wheel_torque_fl}, CoM(wheel_fl)):
> wheel_eqns := simplify([ comp_Y(eqnsEA_wrr,wheel_rr[frame]), comp_Y(eqnsEA_wrl,wheel_rl[frame]),
comp_Y(eqnsEA_wfr,wheel_fr[frame]), comp_Y(eqnsEA_wfl,wheel_fl[frame])]):<%>;
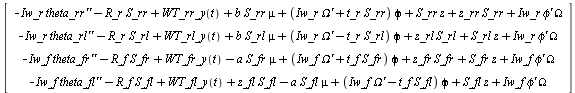(1.2.3.1)
Tire slips relaxations
> U_rr := VS_rr;
> U_rl := VS_rl;
> U_fr := VS_fr;
> U_fl := VS_fl;
(1.2.4.1)
relaxation equatiopns
> slip_eqns := [
sigma_y/U_rr * diff(Lambda_rr(t),t) + Lambda_rr(t) - lambda_rr,
sigma_y/U_rl * diff(Lambda_rl(t),t) + Lambda_rl(t) - lambda_rl,
sigma_y/U_fr * diff(Lambda_fr(t),t) + Lambda_fr(t) - lambda_fr,
sigma_y/U_fl * diff(Lambda_fl(t),t) + Lambda_fl(t) - lambda_fl,
sigma_x/U_rr * diff(Kappa_rr(t),t) + Kappa_rr(t) - kappa_rr,
sigma_x/U_rl * diff(Kappa_rl(t),t) + Kappa_rl(t) - kappa_rl,
sigma_x/U_fr * diff(Kappa_fr(t),t) + Kappa_fr(t) - kappa_fr,
sigma_x/U_fl * diff(Kappa_fl(t),t) + Kappa_fl(t) - kappa_fl
]:
<slip_vars>, <slip_eqns>;
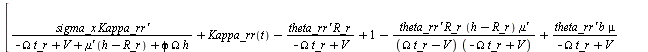
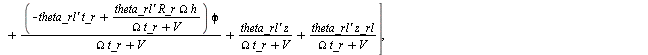
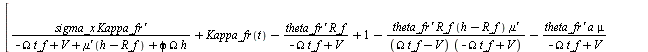
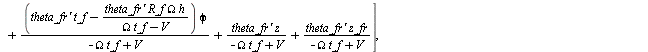
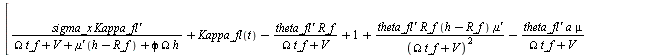
(1.2.4.2)
Road equations
> shortname(s(t),n(t),alpha(t)):
> track_vars := [ s(t),n(t), curvilinear coordinates
alpha(t) ]; relative yaw
(1.2.5.1)
Frame fixed on the road center line
> TR := inv_frame ( Translate(0,n(t),0) . Rotate('Z',alpha(t)) ):
> VR := project(velocity(origin(TR)),TR): show(VR);
(1.2.5.2)
Implicit formulation
> track_eqns := [ diff(s(t),t) - comp_X(VR,TR),
comp_Y(VR,TR),
Theta(s(t))*diff(s(t),t) - comp_Z(angular_velocity(TR)) ]:
> Vector(track_eqns);
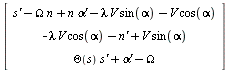(1.2.5.3)
First order formulation
> all_vars := [op(track_vars), op(dyna_vars14), op(slip_vars)];
> all_eqns := [op(track_eqns), op(dyna_eqns14), op(slip_eqns)]:
> nops(all_vars) = nops(all_eqns);
(1.2.6.1)
> pos_vars := suspensions_vars union [z(t),phi(t),mu(t),delta(t)];
> vars_to_fovars := seq(pos_vars[i]=eval(cat(op(0,pos_vars[i]),_dot)(t)),i=1..nops(pos_vars)), seq(wheels_spin[i]=eval(cat(op(0,wheels_spin[i]),_dot)(t)),i=1..nops(wheels_spin));
(1.2.6.2)
> fo_vars := subs(vars_to_fovars,all_vars) union pos_vars ;
> fo_eqns := down_order(all_eqns,pos_vars union wheels_spin,t) union [seq(diff(pos_vars[i],t)-cat(op(0,pos_vars[i]),_dot)(t),i=1..nops(pos_vars))] :
(1.2.6.3)
>
Explicit forces
Aerodynamics
> aero_forces := [ Drag = 1/2*rho*CdA*V(t)^2,
Lift = 1/2*rho*ClA*V(t)^2 ]: <%>;
(1.3.1.1)
Tire vertical forces
> tire_N := 'tire_N':
> tire_N := (name, N0, zw, zw_rate) -> N0 + cat(kt_,name)*zw + cat(ct_,name)*zw_rate ; scaling to keep posReg normalized
(1.3.2.1)
Check static loads
> subs( Drag = 0, Lift_r=0, Lift_f=0,
seq(chassis_vars[i]=0, i=1..nops(chassis_vars)),
seq(grossmotion_vars[i]=0, i=1..nops(grossmotion_vars)),
seq(diff(wheels_spin[i],t,t)=0, i=1..nops(wheels_spin)),
seq(suspensions_vars[i]=0, i=1..nops(suspensions_vars)),
seq(lhs(aero_forces[i])=0, i=1..nops(aero_forces)) ,
N_rl=NR0,N_rr=NR0, N_fl=NF0,N_fr=NF0, [comp_Z(eqnsN), comp_Y(eqnsEA)]):
> static_loads := op(solve(%, [NR0,NF0])): <%>;
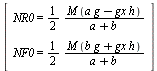(1.3.2.2)
> xi_dot_rr := down_order(diff(xi_rr,t), [z(t),phi(t),mu(t)] union suspensions_vars ,t):
> xi_dot_rl := down_order(diff(xi_rl,t), [z(t),phi(t),mu(t)] union suspensions_vars, t):
> xi_dot_fr := down_order(diff(xi_fr,t), [z(t),phi(t),mu(t)] union suspensions_vars, t):
> xi_dot_fl := down_order(diff(xi_fl,t), [z(t),phi(t),mu(t)] union suspensions_vars, t):
> tires_load := [
N_rr = tire_N(r, NR0, xi_rr, xi_dot_rr),
N_rl = tire_N(r, NR0, xi_rl, xi_dot_rl),
N_fr = tire_N(f, NF0, xi_fr, xi_dot_fr),
N_fl = tire_N(f, NF0, xi_fl, xi_dot_fl)
]: <%>;
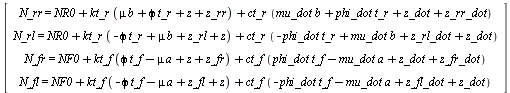(1.3.2.3)
> tires_def := [ zw_rr = xi_rr, zw_rl = xi_rl,
zw_fr = xi_fr, zw_fl = xi_fl,
zw_dot_rr = xi_dot_rr, zw_dot_rl = xi_dot_rl,
zw_dot_fr = xi_dot_fr, zw_dot_fl = xi_dot_fl
]:<%>;
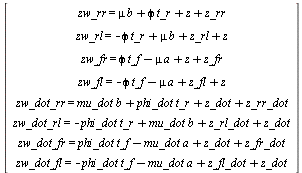(1.3.2.4)
Tire horizontal forces
> tires_camber := [ gamma_rr = camber_rr + gamma_rr0,
gamma_rl = camber_rl - gamma_rr0,
gamma_fr = camber_fr + gamma_fr0,
gamma_fl = camber_fl - gamma_fr0
]:<%>;
(1.3.3.1)
> tires_forces := [
Lateral forces
> F_rr = tire_F(rr,N_rr, Lambda_rr(t), gamma_rr, Kappa_rr(t)),
> F_rl = tire_F(rl,N_rl, Lambda_rl(t), gamma_rl, Kappa_rl(t)),
> F_fr = tire_F(fr,N_fr, Lambda_fr(t), gamma_fr, Kappa_fr(t)),
> F_fl = tire_F(fl,N_fl, Lambda_fl(t), gamma_fl, Kappa_fl(t)),
Longitudinal forces
> S_rr = tire_S(rr,N_rr, Lambda_rr(t), gamma_rr, Kappa_rr(t) ),
> S_rl = tire_S(rl,N_rl, Lambda_rl(t), gamma_rl, Kappa_rl(t) ),
> S_fr = tire_S(fr,N_fr, Lambda_fr(t), gamma_fr, Kappa_fr(t) ),
> S_fl = tire_S(fl,N_fl, Lambda_fl(t), gamma_fl, Kappa_fl(t) )
]: <%>;
Substitute tyres camber angles into forces expressions
> tires_forces := subs(tires_camber,tires_forces):#<%>;
(1.3.3.2)
Define suspensions and antirollbars forces
> suspensions_forces := [
> FSa_rr = suspension_F(r,z_rr(t),z_rr_dot(t)) + kj_r * (z_rr(t) - z_rl(t)),
> FSa_rl = suspension_F(r,z_rl(t),z_rl_dot(t)) - kj_r * (z_rr(t) - z_rl(t)),
> FSa_fr = suspension_F(f,z_fr(t),z_fr_dot(t)) + kj_f * (z_fr(t) - z_fl(t)),
> FSa_fl = suspension_F(f,z_fl(t),z_fl_dot(t)) - kj_f * (z_fr(t) - z_fl(t))
> ]: <%>;
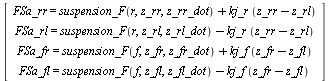(1.3.4.1)