Pendulum with elasti joint
> restart: libname := libname, "C:/MBSymba": with(MBSymba_r6):
> PDEtools[declare]([x(t),y(t),theta(t)],prime=t,quiet):

body definition
Define the body frame
> T1 := translate(x(t),y(t),0) . rotate('Z',theta(t)) ;
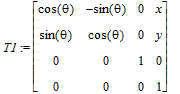
Define the body
> pendulum := make_BODY(T1,m,0,0,IG): show(pendulum);

Define acceleration due to gravity
> _gravity := make_VECTOR(ground,0,-g,0): show(_gravity);

ELASTIC pin joint
Let's first define a rigig joint
Define the pin joint A
> A := make_POINT(T1,0,L,0): show(A);
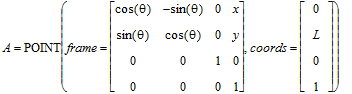
> PDEtools[declare]([FxA(t),FyA(t)],prime=t,quiet):
FzA(t):=0; planar system
> revj_A, FA := spherical_JOINT( A,origin(ground),pendulum,"A"): show(revj_A); show(FA);
![]()


To convert the rigid joint into a flexible one it is sufficient to define reaction forces proportionally to the constraints violation, as follows:
> elastic_joint := seq( revj_A[vars][i] = k*revj_A[expr][i] + c*diff(revj_A[expr][i],t), i=1..2);
![]()
and substitute it into the reaction force
> FA[comps] := subs(elastic_joint,FA[comps]): show(FA);
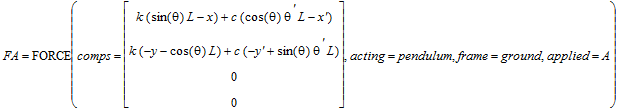
Newton's equations
> eqnsN := newton_equations({ pendulum, FA}): show(eqnsN);

Euler's equations with respect to the point A, in moving frame
> eqnsE := euler_equations({ pendulum, FA},CoM(pendulum)): show(eqnsE);
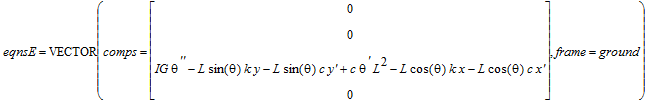
> eqnsNE := [comp_Z(eqnsE), comp_X(eqnsN),comp_Y(eqnsN)]: 'eqnsNE'=Vector(%);
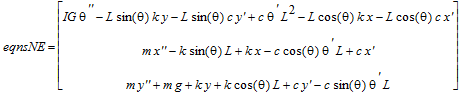
Numerical solution
> interface(displayprecision=2):
> params:= [L=1,IG=1,m=3,g=9.81, k=1500,c=1];
![]()
> IC := {theta(0)=0,D(theta)(0)=0, x(0)= 0.02, D(x)(0)=0, y(0)=-1, D(y)(0)=0};
![]()
> sys:= convert(subs(params,eqnsNE),set) union IC:
solz:= dsolve(sys,numeric,range=0..4):
> npt:=500:
plots[odeplot](solz, [t,theta(t)], color=blue,labels=["t","theta"],numpoints=npt);
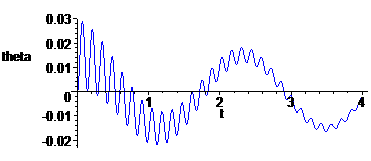
> plots[odeplot](solz, subs(params,[comp_X(A,ground), comp_Y(A,ground)]), color=red, numpoints=npt,scaling=constrained, labels=["x","y"], title="pin joint displacement");
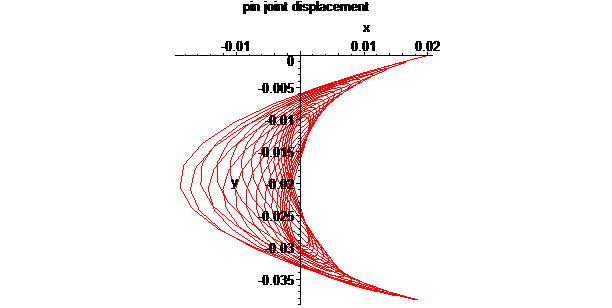
>
>