> restart: libname := libname, "C:/libs/MBSymba.mla": with(MBSymba_r6):

In MBSymba, each Cartesian reference frames is described by means of a 4x4 transformation matrix T.

Such matrix embeds the frame orientation (3x3 rotation matrix R) and frame origin (3x1 vector A) with respect a unique master frame, which is by default an inertial reference frame called ground.

> show(ground);

Reference frames may easily be contructed by combining basic rotation and translation operators

Translation operator

translational operator translate

> TA := translate(xA,yA,zA);

Rotation operators

rotation operator rotate

rotation about X axis by phi

> Rx := rotate('X',phi);

> evalm(Rx &* P);

rotation around Y axis by mu and around Z axis by psi

> Ry := rotate('Y',mu);
Rz := rotate('Z',psi);

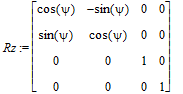
Combination of Transformations

> alias (S=sin,C=cos);

transformations may be combined by multiplying basic transformation operators, starting from left to right

Example

> psi, phi, mu; yaw, roll and pitch angle

overall transformation matrix is

> TT := rotate('Z',psi) * rotate('X',phi) * rotate('Y',mu);

BE CAREFUL: transformation concatenation is not commutative, a change in the transformation order yields a different transformation matrix
example:

> rotate('X',phi) * rotate('Y',mu);
rotate('Y',mu) * rotate('X',phi);

Angular velocity

If you define a time variant transformation matrix

> TT := rotate('X',phi(t)) * rotate('Y',mu(t));

you may easy compute the angular velocity as follows:

> Omega := angular_velocity(TT): show(Omega);