> restart: libname := `C:/MBSymba`, libname: with(MBSymba_r6):

> #alias(S=sin,C=cos):

Angular velocity

> PDEtools[declare](psi(t),phi(t),mu(t), prime=t, quiet):

> T := Rotate('Z',psi(t)) . Rotate('X',phi(t));

velocity matrix

> W := simplify( inv_frame(T) . map(diff,T,t) );

> omega := angular_velocity(T): show(omega);

> TYRP := T . Rotate('Y',mu(t));

eqns

> Vector([omega[X],omega[Y],omega[Z]]) = omega[comps];

> eqns := [omega[X] = comp_X(omega), omega[Y] = comp_Y(omega), omega[Z]=comp_Z(omega)]:

> op(solve(eqns, diff([psi(t),phi(t),mu(t)],t))): Vector(%);

>

Angular velocity: Bryant's angles

> PDEtools[declare](rx(t),ry(t),rz(t), prime=t, quiet);

> TC := Rotate('X',rx(t)) . Rotate('Y',ry(t)) . Rotate('Z',rz(t));

> Omega := angular_velocity(TC): show(Omega);

> eqns := [omega[X] = comp_X(Omega), omega[Y] = comp_Y(Omega), omega[Z]=comp_Z(Omega)]:
angvel := solve(eqns,diff([rx(t),ry(t),rz(t)],t))[1]: Vector(angvel);

Angular velocity: yaw-roll-picth angles

> PDEtools[declare](psi(t),phi(t),mu(t), prime=t, quiet);
TYRP := rotate('Z',psi(t)) * rotate('X',phi(t)) * rotate('Y',mu(t));

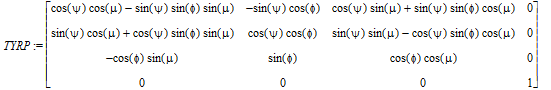
> Omega := angular_velocity(TYRP): show(Omega);

> eqns := [omega[X] = comp_X(Omega), omega[Y] = comp_Y(Omega), omega[Z]=comp_Z(Omega)]:
angvel := solve(eqns,diff([psi(t),phi(t),mu(t)],t))[1]: Vector(angvel);